Dasar-Dasar Visualisasi dengan Seaborn

Setelah kita mempersiapkan lingkungan dan dataset iris, mari kita lanjutkan dengan memahami dasar-dasar visualisasi data menggunakan Seaborn.

Sebelum kita menjelajahi teknik visualisasi lanjutan, mari kita memahami dasar-dasar penggunaan Seaborn. Sebagai pengantar, kita akan menggunakan dataset iris yang telah kita persiapkan sebelumnya.

A. Pengenalan API Seaborn

#

Seaborn menyediakan antarmuka yang intuitif melalui API-nya untuk menciptakan berbagai jenis plot. Mari kita mulai dengan membuat scatter plot yang sederhana untuk mengeksplorasi hubungan antara sepal length dan sepal width dari bunga iris.

Pertama-tama, kita akan membahas cara membuat scatter plot menggunakan Seaborn. Scatter plot adalah salah satu jenis plot yang sering digunakan untuk mengeksplorasi hubungan antara dua variabel. Dengan menggunakan fungsi sns.scatterplot(), kita dapat dengan mudah memvisualisasikan seberapa baik kita dapat membedakan spesies bunga iris berdasarkan sepal length dan sepal width mereka.

# Scatter plot menggunakan Seaborn
sns.scatterplot(x='sepal length (cm)', y='sepal width (cm)', data=iris_df, hue='species', palette='viridis')
plt.title('Scatter Plot antara Sepal Length dan Sepal Width')
plt.show()

Hasilnya:

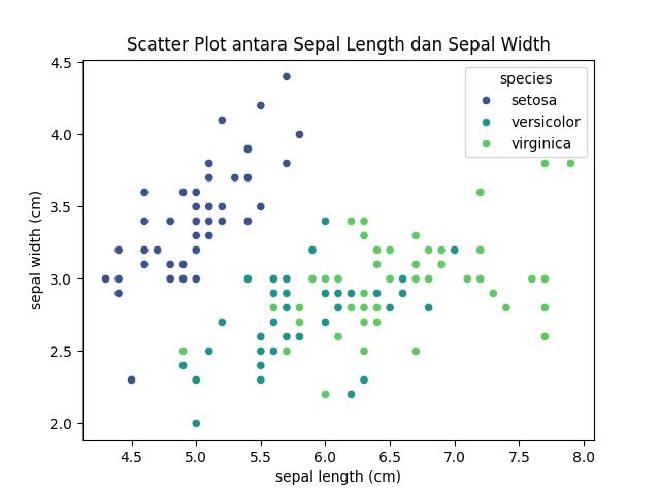
Plot ini memvisualisasikan seberapa baik kita dapat membedakan tiga spesies bunga iris berdasarkan sepal length dan sepal width mereka. Warna yang berbeda mengindikasikan spesies yang berbeda.

B. Menambah Dimensi dengan Palettes dan Markers

#

Selanjutnya, kita dapat menambahkan dimensi tambahan ke plot ini menggunakan palettes dan markers yang disediakan oleh Seaborn. Kita akan mempelajari penggunaan palettes dan markers pada scatter plot. Dengan menyesuaikan warna dan jenis marker, kita dapat menambah dimensi tambahan ke dalam plot, membuatnya lebih informatif dan menarik.

# Scatter plot dengan palettes dan markers
sns.scatterplot(x='sepal length (cm)', y='sepal width (cm)', data=iris_df, hue='species', palette='viridis', style='species', s=100)
plt.title('Scatter Plot dengan Palettes dan Markers')
plt.show()

Hasilnya:

Pada contoh ini, kita menggunakan markers untuk membedakan spesies bunga iris, dan palettes viridis untuk memberikan warna yang lebih menarik pada plot.

C. Histogram dan KDE (Kernel Density Estimation)

#

Terakhir, kita akan mempelajari penggunaan histogram dan KDE untuk memvisualisasikan distribusi variabel. Dalam contoh ini, kita akan fokus pada sepal length dan membandingkan distribusinya di antara spesies bunga iris.

Seaborn juga menyediakan fungsi untuk membuat histogram dan KDE secara bersamaan. Contoh di bawah ini memvisualisasikan distribusi dari sepal length untuk setiap spesies.

# Histogram dan KDE untuk sepal length
sns.histplot(data=iris_df, x='sepal length (cm)', kde=True, hue='species', element='step', stat='density', common_norm=False)
plt.title('Histogram dan KDE untuk Sepal Length')
plt.show()

Hasilnya:

Plot ini memberikan pandangan lebih dalam tentang sebaran sepal length pada setiap spesies dengan menggunakan histogram dan KDE secara bersamaan.

D. Sekilas Tentang KDE

#

KDE atau Kernel Density Estimation adalah metode statistik non-parametrik yang digunakan untuk memperkirakan fungsi kepadatan probabilitas (probability density function - PDF) dari suatu variabel acak. Pada konteks visualisasi data dengan Seaborn atau library visualisasi data lainnya, KDE sering digunakan untuk memperkirakan distribusi data secara lebih halus.

Berikut adalah beberapa poin penting terkait dengan KDE:

• Fungsi Kepadatan Probabilitas (PDF): KDE memberikan perkiraan visual dari distribusi probabilitas suatu variabel. Fungsi ini memberikan gagasan tentang sebaran data dan diplot sebagai kurva kontinu.

• Non-Parametrik: Metode non-parametrik berarti KDE tidak mengasumsikan bentuk tertentu dari distribusi data. Sebaliknya, ia membangun distribusi yang paling sesuai berdasarkan data yang diberikan.

• Kernel: “Kernel” dalam KDE adalah fungsi yang ditempatkan di setiap titik data dan digunakan untuk membentuk distribusi. Umumnya, kernel Gauss atau Epanechnikov digunakan, tetapi ada berbagai pilihan kernel yang dapat dipilih tergantung pada karakteristik data.

• Smoothing: Salah satu keuntungan utama KDE adalah kemampuannya untuk meratakan fluktuasi acak dalam data, membuat distribusi lebih halus dan lebih mudah untuk diinterpretasikan. Proses ini sering disebut sebagai smoothing.

Secara matematis, PDF yang diestimasi dengan KDE dapat diwakili sebagai konvolusi dari kernel yang ditempatkan di setiap titik data:

$$f(x) = \frac{1}{n\cdot h}\sum_{1}^{i=1} K(\frac{x-x_i}{h})$$

Dimana \(f(x)\) adalah PDF yang diestimasi, \(x_i\) adalah titik data, \(K\) adalah kernel, dan \(h\) adalah bandwidth yang mengontrol seberapa “lebar” distribusi hasilnya.

Dengan menggunakan KDE dalam visualisasi data, kita dapat dengan lebih mulus memahami distribusi dan kecenderungan dalam dataset kita. Seaborn secara otomatis menggunakan KDE pada beberapa plot, seperti pada histogram di bagian sebelumnya, untuk memberikan gambaran visual yang lebih halus tentang distribusi variabel.

Dengan memahami konsep-konsep dasar ini, kita dapat memahami lebih banyak fitur Seaborn untuk membuat visualisasi data yang informatif dan menarik.