
Dasar-Dasar Linear Regression
Table of Contents
Pemodelan Linear Regression - This article is part of a series.
Pada bagian ini, kita akan mempelajari secara rinci dasar-dasar Linear Regression, termasuk konsep dependent variable (variabel terikat) dan independent variable (variabel bebas), persamaan Linear Regression, konsep garis regresi, dan koefisien regresi. Pembahasan ini akan memberikan pemahaman mendalam tentang elemen-elemen penting dalam Linear Regression.
A. Variabel Terikat dan Variabel Bebas #
Dalam Linear Regression, pemahaman konsep variabel terikat dan variabel bebas merupakan langkah awal yang sangat penting. Keduanya memainkan peranan penting dalam membentuk hubungan linier dan memprediksi nilai variabel terikat berdasarkan nilai variabel bebas.
1. Variabel Terikat (Dependent Variable) #
Variabel terikat adalah variabel yang ingin kita prediksi atau ukur nilai-nilainya. Dalam konteks Linear Regression, variabel terikat biasanya ditempatkan pada sumbu \(\mathbf{Y}\) dalam persamaan regresi. Misalnya, jika kita memodelkan harga rumah, harga rumah akan menjadi variabel terikat karena kita tertarik untuk memprediksi nilai harga berdasarkan variabel bebas tertentu.
2. Variabel Bebas (Independent Variable) #
Variabel bebas adalah variabel yang digunakan untuk membuat prediksi atau menjelaskan variasi dalam variabel terikat. Variabel bebas ditempatkan pada sumbu \(\mathbf{X}\) dalam persamaan regresi. Dalam contoh harga rumah, variabel bebas bisa menjadi jumlah kamar, luas tanah, atau fitur-fitur lain yang mempengaruhi harga rumah.
3. Hubungan Antara Variabel Terikat dan Bebas #
Linear Regression bertujuan untuk mengukur dan memodelkan hubungan linier antara variabel terikat dan variabel bebas. Ketika kita memahami hubungan ini, kita dapat menggunakan model Linear Regression untuk membuat prediksi tentang nilai variabel terikat berdasarkan nilai variabel bebas.
C. Konsep Garis Regresi #
Konsep garis regresi adalah visualisasi geometris dari hubungan linier antara variabel terikat (\(\mathbf{Y}\)) dan variabel bebas (\(\mathbf{X}\)) dalam model Linear Regression. Garis ini memberikan gambaran tentang pola umum dalam data dan membantu dalam membuat prediksi berdasarkan model yang dibentuk.
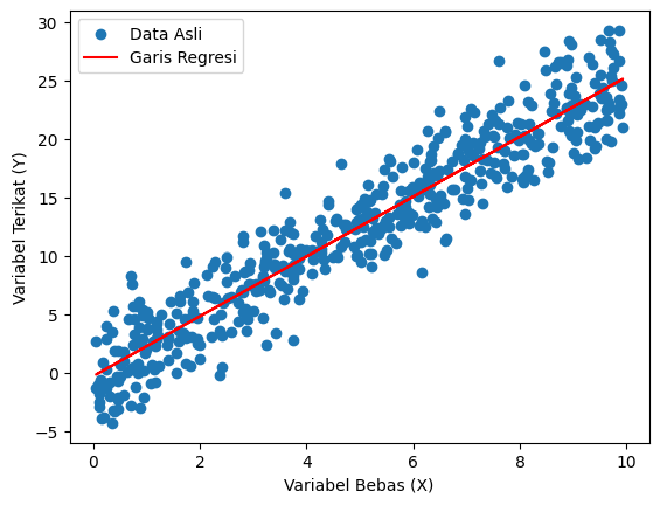
1. Membentuk Garis Regresi #
Garis regresi dibentuk dengan mencocokkan model Linear Regression ke data. Tujuannya adalah untuk menemukan garis terbaik yang meminimalkan jumlah kuadrat residual \(\epsilon\) (jarak antara nilai yang diamati dan nilai yang diprediksi oleh model).
2. Tujuan Garis Regresi #
- Mewakili hubungan linier antara variabel bebas dan variabel terikat.
- Memberikan alat visual untuk memahami arah dan kekuatan hubungan.
- Membuat prediksi tentang nilai variabel terikat berdasarkan nilai variabel bebas.
3. Pemodelan Hubungan Linier #
- Jika garis regresi cenderung naik dari kiri ke kanan, ini menunjukkan hubungan positif.
- Jika garis regresi cenderung turun dari kiri ke kanan, ini menunjukkan hubungan negatif.
- Semakin miring garis, semakin besar efek variabel bebas terhadap variabel terikat.
4. Evaluasi Kualitas Garis Regresi #
- Jarak Residual: Memeriksa sebaran residual (jarak vertikal antara titik data dan garis regresi). Sebaran yang seragam menunjukkan homoskedastisitas.
- Analisis Outlier: Identifikasi titik data yang mungkin merupakan outlier dan mempengaruhi bentuk garis regresi.
- R-squared (\(R^2\)): Mengukur seberapa baik garis regresi cocok dengan data. Nilai \(R^2\) mendekati 1 menunjukkan kecocokan yang baik.
Garis regresi adalah alat visual yang kuat dalam mewakili hubungan linier antara variabel bebas dan variabel terikat. Memahami konsep ini membantu penafsiran model Linear Regression dan memfasilitasi pengambilan keputusan berdasarkan prediksi yang dihasilkan. Visualisasi dengan menggunakan garis regresi juga mempermudah komunikasi hasil analisis kepada pemangku kepentingan yang mungkin tidak akrab dengan teknikalitas model statistik.
D. Jenis-jenis Linear Regression #
Linear Regression memiliki berbagai variasi atau jenis, yang masing-masing memiliki penggunaan dan asumsi yang berbeda-beda. Berikut adalah beberapa jenis Linear Regression yang umum digunakan:
1. Simple Linear Regression: #
- Deskripsi: Simple Linear Regression melibatkan hubungan linier antara satu variabel bebas (\(\mathbf{X}\)) dan satu variabel terikat (\(\mathbf{Y}\)).
- Persamaan: \[ \mathbf{Y} = \beta_0 + \beta_1 \mathbf{X} + \varepsilon \]
- Aplikasi: Digunakan ketika hubungan antara dua variabel dapat dijelaskan secara sederhana.
2. Multiple Linear Regression: #
- Deskripsi: Multiple Linear Regression melibatkan hubungan linier antara dua atau lebih variabel bebas (\(\mathbf{X}_1, \mathbf{X}_2, \ldots, \mathbf{X}_n\)) dan satu variabel terikat (\(\mathbf{Y}\)).
- Persamaan: \[ \mathbf{Y} = \beta_0 + \beta_1\mathbf{X}_1 + \beta_2\mathbf{X}_2 + \ldots + \beta_n\mathbf{X}_n + \varepsilon \]
- Aplikasi: Digunakan ketika terdapat lebih dari satu variabel bebas yang mempengaruhi variabel terikat.
3. Ridge Linear Regression: #
- Deskripsi: Ridge Linear Regression adalah varian dari Linear Regression berganda yang dirancang untuk mengatasi masalah multikolinieritas (korelasi tinggi antara variabel bebas).
- Penyesuaian: \[\mathbf{J} = \sum_{i=1}^{n} (Y_i - (\beta_0 + \beta_1X_{1i} + \beta_2X_{2i} + \ldots + \beta_nX_{ni}))^2 + \alpha \sum_{j=1}^{n} \beta_j^2 \]
- Aplikasi: Berguna ketika terdapat korelasi tinggi antara variabel bebas.
4. Lasso Linear Regression: #
- Deskripsi: Lasso Linear Regression (Least Absolute Shrinkage and Selection Operator) digunakan untuk mereduksi jumlah variabel bebas yang signifikan, menerapkan penalti L1.
- Penyesuaian: \[ \mathbf{J} = \sum_{i=1}^{n} (Y_i - (\beta_0 + \beta_1X_{1i} + \beta_2X_{2i} + \ldots + \beta_nY_{ni}))^2 + \alpha \sum_{j=1}^{n} |\beta_j| \]
- Aplikasi: Berguna untuk seleksi fitur (feature selection) dalam model.
5. ElasticNet Linear Regression: #
-
Deskripsi: ElasticNet Linear Regression merupakan gabungan dari Ridge Linear Regression dan Lasso Linear Regression, yaitu menggabungkan penalti L1 dan L2.
-
Penyesuaian: $$ \mathbf{J} = \sum_{i=1}^{n} \left( Y_i - (\beta_0 + \beta_1X_{1i} + \beta_2X_{2i} + \ldots + \beta_nX_{ni})\right)^2 + \alpha \sum_{j=1}^{n} (\lambda|\beta_j| + (1-\lambda)\beta_j^2) $$
-
Aplikasi: Berguna ketika terdapat korelasi tinggi antara variabel bebas dan beberapa variabel bebas tidak relevan.
Jenis-jenis Linear Regression memberikan fleksibilitas dalam menangani berbagai situasi dan karakteristik data. Pemilihan jenis regresi yang tepat tergantung pada sifat dataset, asumsi yang diinginkan, dan tujuan analisis.
E. Contoh Penerapan Linear Regression #
Sebagai contoh, bayangkan kita ingin memprediksi hasil ujian (\(\mathbf{Y}\)) berdasarkan jumlah jam belajar (\(\mathbf{X}\)). Dalam hal ini, hasil ujian adalah variabel terikat karena kita ingin memprediksi nilainya. Jumlah jam belajar menjadi variabel bebas yang dapat mempengaruhi hasil ujian. Dengan menggunakan Linear Regression, kita dapat memodelkan hubungan linier antara kedua variabel ini untuk membuat prediksi yang lebih akurat.
Beberapa contoh penerapan lainnya:
-
Prediksi Produksi Tanaman:
- Variabel Terikat: Produksi tanaman.
- Variabel Bebas: Jumlah hujan.
- Penerapan: Memprediksi produksi tanaman berdasarkan jumlah hujan.
-
Prediksi Penjualan Produk:
- Variabel Terikat: Penjualan produk.
- Variabel Bebas: Jumlah iklan.
- Penerapan: Memprediksi penjualan produk berdasarkan jumlah iklan yang dilakukan.
Pemahaman yang jelas tentang peran dan hubungan antara variabel terikat dan bebas sangat penting dalam merancang dan menginterpretasikan model Linear Regression. Dengan merinci konsep ini, kita dapat lebih efektif menerapkan Linear Regression dalam konteks analisis data dan prediksi.

