Simple Linear Regression

Simple Linear Regression (SLR) adalah metode statistik yang digunakan untuk memodelkan hubungan linier antara satu variabel bebas (\(X\)) dan satu variabel terikat (\(Y\)). Dalam konteks ini, kita mencoba menemukan garis regresi terbaik yang dapat memprediksi nilai \(Y\) berdasarkan nilai \(X\).

A. Persamaan Simple Linear Regression (SLR)

#

Persamaan SLR merupakan representasi matematis dari hubungan linier antara satu variabel bebas (\(X\)) dan satu variabel terikat (\(Y\)). Persamaan ini memungkinkan kita untuk memodelkan seberapa besar perubahan dalam variabel terikat (\(Y\)) yang dapat diatribusikan kepada perubahan dalam variabel bebas (\(Y\)).

Berikut adalah persamaan SLR:

\[ Y = \beta_0 + \beta_1 X + \varepsilon, \tag{3.3.1}\]

dimana:

• \(Y\): Variabel terikat yang ingin diprediksi.
• \(\beta_0\): Intercept, yaitu nilai \(Y\) ketika \(X\) sama dengan nol.
• \(\beta_1\): Koefisien kemiringan yang menunjukkan seberapa besar perubahan yang diharapkan dalam \(Y\) untuk setiap penambahan satu unit dalam \(X\).
• \(X\): Variabel bebas yang mempengaruhi \(\mathbf{y}\).
• \(\varepsilon\): Kesalahan atau residual, yang merepresentasikan faktor-faktor yang tidak dapat dijelaskan oleh model.

Perhatikan persamaan \((3.3.1)\) di atas. Persamaan ini mengandung variabel \(\varepsilon\) yang merupakan kesalahan atau residual. Jika kita menghilangkan variabel \(\varepsilon\), maka kita bisa menuliskan prediksi dari variabel \(Y\) sebagai: \[ \hat{Y} = \hat{\beta}_0 + \hat{\beta}_1 X. \tag{3.3.2}\]

Perlu diperhatikan bahwa variabel \(\hat{Y} \) merupakan estimasi dari variabel \(Y\). Nilainya tidak exact sama dengan sebenernya. Sedangkan \(\hat{\beta}_0\) dan \(\hat{\beta}_1\) merupakan estimasi dari \(\beta_0\) dan \(\beta_1\) secara berturut-turut.

Persamaan SLR memiliki dua koefisien utama, yaitu intercept (\(\beta_0\)) dan koefisien kemiringan (\(\beta_1\)). Mari kita bahas lebih detail tentang kedua koefisien ini:

1. Intercept (\(\beta_0\))

#

Intercept adalah nilai \(Y\) ketika \(X\) sama dengan nol. Dalam konteks persamaan SLR, koefisien ini adalah titik di mana garis regresi memotong sumbu \(Y\).

Jika \(\beta_0\) positif, itu menunjukkan bahwa ketika variabel bebas (\(X\)) sama dengan nol, variabel terikat (\(Y\)) memiliki nilai positif. Sebaliknya, jika \(\beta_0\) negatif, variabel terikat memiliki nilai negatif saat \(X\) sama dengan nol.

2. Koefisien Kemiringan (\(\beta_1\)):

#

Koefisien kemiringan (\(\beta_1\)) mengukur seberapa besar perubahan yang diharapkan dalam variabel terikat (\(Y\)) untuk setiap penambahan satu unit dalam variabel bebas (\(X\)).

Jika \(\beta_1\) positif, ini menunjukkan hubungan positif antara \(X\) dan \(Y\); seiring \(X\) meningkat, \(Y\) cenderung meningkat juga. Sebaliknya, jika \(\beta_1\) negatif, hubungan antara \(X\) dan \(Y\) bersifat negatif.

B. Estimasi Koefisien \(\beta_0\) dan \(\beta_1\) Menggunakan Least Square

#

Estimasi koefisien merupakan proses menghitung nilai perkiraan (\(\hat{\beta}\)) dari parameter koefisien dalam model. Proses estimasi ini melibatkan pendekatan numerik untuk mencari nilai yang optimal. Meskipun untuk SLR, terdapat solusi analitik yang dapat dihitung secara langsung, dalam kasus Linear Regression berganda atau model yang lebih kompleks, solusi analitik mungkin tidak praktis atau bahkan tidak memungkinkan. Pada Linear Regression, estimasi koefisien (\(\hat{\beta}_0\) untuk Intercept dan \(\hat{\beta}_1\) untuk koefisien kemiringan) diperoleh dengan menggunakan metode Least Squares.

Least Squares adalah metode optimasi yang digunakan untuk menemukan garis atau model regresi yang memberikan jumlah kuadrat residual (perbedaan antara nilai sebenarnya dan nilai yang diprediksi) yang paling kecil. Tujuan metode Least Squares adalah meminimalkan jumlah kuadrat residual, yaitu jumlah kuadrat perbedaan antara nilai sebenarnya (\(Y_i\)) dan nilai yang diprediksi oleh model (\(\hat{Y}_i\)) menggunakan persamaan \((3.3.1)\) di atas.

Formula dari metode Least Squares adalah sebagai berikut: \[ L = \sum_{i=1}^{n} (Y_i - \hat{Y}_i)^2, \tag{3.3.3}\]

dimana \(n\) adalah jumlah sampel dalam dataset. Dengan melakukan subtitusi persamaan \((3.3.2)\) ke dalam persamaan \((3.3.3)\), maka diperoleh: \[ L = \sum_{i=1}^{n} (Y_i - \hat{\beta}_0 + \hat{\beta}_1 X_i)^2. \tag{3.3.4}\]

Untuk mendapatkan estimasi dari variabel \(\beta_0\) dan \(\beta_1\), kita bisa memanfaatkan turunan parsial. Nilai \(L\) akan mencapai minimum ketika turunan parsial dari \(L\) bernilai 0, yaitu \(\frac{\partial L}{\partial \hat{\beta}_0}=0\) dan \(\frac{\partial L}{\partial \hat{\beta}_1}=0\).

Berikut adalah penjabaran untuk \(\frac{\partial L}{\partial \hat{\beta}_0}=0\):

\[-2 \sum_{i=1}^{n} (Y_i - \hat{\beta}_0 - \hat{\beta}_1 X_i)=0. \tag{3.3.5}\]

Sedangkan untuk \(\frac{\partial L}{\partial \hat{\beta}_1}=0\) diperoleh:

\[ -2 \sum_{i=1}^{n} X_i (Y_i - \hat{\beta}_0 - \hat{\beta}_1 X_i) =0. \tag{3.3.6}\]

Dengan menyelesaikan persamaan \((3.3.5)\) dan \((3.3.6)\) untuk \(\hat{\beta}_0\) dan \(\hat{\beta}_1\), diperoleh:

\[ \hat{\beta}_0 = \bar{Y} - \hat{\beta}_1 \bar{X} \tag{3.3.7} \]

dan

\[ \hat{\beta}_1 = \frac{\sum (X_i - \bar{X})(Y_i - \bar{Y})}{\sum (X_i - \bar{X})^2}, \tag{3.3.8}\]

dimana \(\bar{X}=\sum_{i=1}^{n} \frac{X_i}{n}\) dan \(\bar{Y}=\sum_{i=1}^{n} \frac{Y_i}{n}\) merupakan rata-rata dari \(X\) dan \(Y\).

C. Evaluasi Model

#

Evaluasi dari SLR melibatkan pengukuran kinerja model regresi linear terhadap data pengujian. Beberapa metrik evaluasi umum digunakan dalam konteks SLR untuk mengukur seberapa baik model dapat memprediksi variabel terikat. Berikut adalah beberapa metrik evaluasi utama:

1. Mean Squared Error (MSE):

#

• Deskripsi: MSE mengukur rata-rata dari kuadrat selisih antara nilai terukur dan nilai prediksi dari model.
• Formula: \(\text{MSE} = \frac{1}{n} * \sum (Y_i - \hat{Y}_i)^2\).
• Interpretasi: Semakin kecil nilai MSE, semakin baik model dalam memprediksi data. MSE memberikan informasi tentang seberapa dekat prediksi model dengan nilai terukur.

2. Root Mean Squared Error (RMSE):

#

• Deskripsi: RMSE adalah akar kuadrat dari MSE dan memberikan besaran kesalahan yang lebih terukur dalam satuan asli variabel terikat.
• Formula: \(\text{RMSE} = \sqrt{\text{MSE}}\)
• Interpretasi: Seperti MSE, semakin kecil nilai RMSE, semakin baik model dalam memprediksi data.

3. Mean Absolute Error (MAE):

#

• Deskripsi: MAE mengukur rata-rata dari nilai absolut selisih antara nilai terukur dan nilai prediksi dari model.
• Formula: \(\text{MAE} = \frac{1}{n} * \sum |Y_i - \hat{Y}_i|\).
• Interpretasi: MAE memberikan informasi tentang rata-rata besar kesalahan prediksi dalam satuan asli variabel terikat.

4. Coefficient of Determination (R-squared):

#

• Deskripsi: R-squared mengukur seberapa baik variabilitas dalam variabel terikat dapat dijelaskan oleh model. Nilai R-squared berkisar antara 0 dan 1, di mana 1 menunjukkan model yang sempurna.
• Formula: \(R^2 = 1 - \frac{\sum(Y_i - \hat{Y}_i)^2}{\sum (Y_i - \bar{Y})^2}\), di mana \(\bar{Y}\) adalah rata-rata nilai.
• Interpretasi: Nilai R-squared mendekati 1 menunjukkan bahwa model dapat menjelaskan sebagian besar variabilitas dalam data.

Evaluasi model SLR memerlukan kombinasi dari metrik-metrik ini untuk memberikan pemahaman yang holistik tentang kualitas dan kinerja model terhadap data. Perlu diingat bahwa pemilihan metrik evaluasi dapat bergantung pada tujuan spesifik analisis dan karakteristik data.

D. Implementasi Simple Linear Regression Menggunakan Python

#

Pada bagian ini, kita akan mencoba mengimplementasikan model SLR menggunakan library NumPy. Berikut adalah implementasinya.

import numpy as np
import matplotlib.pyplot as plt

# Fungsi untuk regresi linear sederhana
def simple_linear_regression(X, Y):
    n = len(X)

    # Menghitung rata-rata X dan Y
    mean_X = np.mean(X)
    mean_Y = np.mean(Y)

    # Menghitung koefisien kemiringan (beta_1) dan intercept (beta_0)
    beta_1 = np.sum((X - mean_X) * (Y - mean_Y)) / np.sum((X - mean_X)**2)
    beta_0 = mean_Y - beta_1 * mean_X

    return beta_0, beta_1

# Fungsi untuk membuat prediksi menggunakan model regresi
def predict(X, beta_0, beta_1):
    return beta_0 + beta_1 * X

# Fungsi untuk menghitung rata-rata kesalahan kuadrat (MSE)
def mean_squared_error(Y_true, Y_pred):
    return np.mean((Y_true - Y_pred)**2)

# Generate data contoh dengan 500 titik
np.random.seed(42)
X = np.random.rand(500) * 10
Y = 2 * X + 1 + np.random.randn(500) * 2

# Menghitung koefisien regresi
beta_0, beta_1 = simple_linear_regression(X, Y)

# Membuat prediksi
Y_pred = predict(X, beta_0, beta_1)

# Visualisasi hasil
plt.scatter(X, Y, label='Data Asli')
plt.plot(X, Y_pred, color='red', label='Linear Regression')
plt.xlabel('Variabel Bebas (X)')
plt.ylabel('Variabel Terikat (Y)')
plt.legend()
plt.show()

print(f'beta_0: {beta_0}')
print(f'beta_1: {beta_1}')

# Menghitung dan menampilkan Mean Squared Error (MSE)
mse = mean_squared_error(Y, Y_pred)
print(f'Mean Squared Error: {mse}')

Pada implementasi diatas, kita menggunakan NumPy untuk operasi matematika. Pertama, kita membangkitkan 500 sampel data menggunakan fungsi np.random() untuk pasangan data \(X\) dan \(Y\). Fungsi simple_linear_regression menghitung koefisien regresi (Intercept dan garis kemiringan) sedangkan fungsi predict digunakan untuk membuat prediksi berdasarkan model, dan mean_squared_error menghitung MSE untuk mengevaluasi kinerja model.

Berikut adalah output dari program di atas:

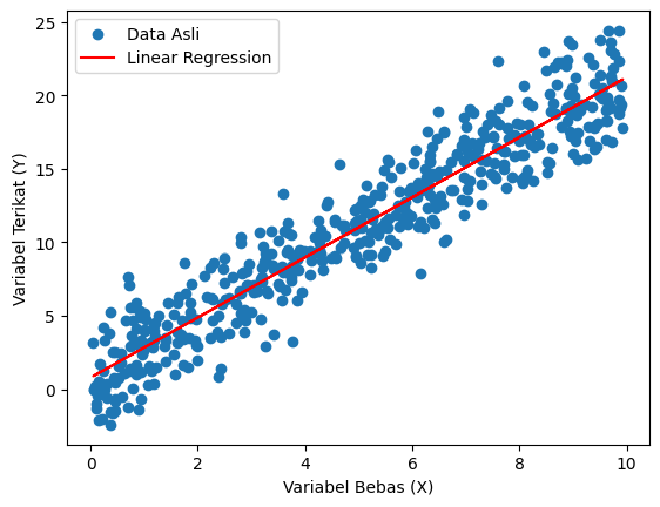
beta_0: 0.7858967069661293
beta_1: 2.0460009245782884
Mean Squared Error: 4.029742481846333

Titik-titik biru pada grafik di atas adalah titik sampel. Sedangkan garis merah merupakan Linear Regression. Estimasi parameter model adalah \(\beta_0=0.7858967069661293\) dan \(\beta_1 = 2.0460009245782884\). Hasil evaluasi model menggunakan MSE adalah \(4.029742481846333\).