Dasar-Dasar Regresi Logistik

Regresi Logistik mengandung konsep-konsep kunci yang menjadi dasar pemahaman dan penerapannya. Pada bagian ini, kita akan membahas elemen-elemen dasar yang membedakan Regresi Logistik dari metode regresi lainnya.

A. Konsep Dasar

#

1. Apa itu Regresi Logistik

#

Regresi Logistik dan Regresi Linear memiliki konsep dasar yang sama, akan tetapi Regresi Logistik lebih cocok digunakan untuk menangani kasus dimana variabel dependen merupakan variabel biner. Kita akan memahami perbedaan ini dan kapan Regresi Logistik lebih sesuai.

Berikut adalah rangkuman perbedaan antara Regresi Linear dan Regresi Logistik:

1. Regresi Linear: Cocok untuk variabel dependen kontinu. Memodelkan hubungan linier antara variabel independen dan dependen. Contohnya: harga saham, suhu, atau pendapatan.

2. Regresi Logistik: Cocok untuk variabel dependen biner. Memodelkan probabilitas kejadian satu dari dua kategori. Contohnya: apakah pelanggan membeli produk (1) atau tidak (0).

2. Log-Odds dan Transformasi Logit

#

Konsep log-odds dan transformasi logit menjadi bagian penting dari Regresi Logistik untuk memahami dan menginterpretasikan hubungan antara variabel independen dan variabel dependen biner.

a. Log-Odds

#

Log-odds adalah logaritma dari odds, yang merupakan rasio probabilitas kejadian terjadi dengan probabilitas kejadian tidak terjadi.

Dinyatakan sebagai: $$\text{Log-Odds} = log\left(\frac{p}{1-p}\right)$$

dimana \(p\) adalah probabilitas kejadian.

b. Transformasi Logit

#

Transformasi logit adalah cara mengonversi probabilitas (\(p\)) menjadi skala log-odds.

Dinyatakan sebagai:

$$ \text{Transformasi Logit} = log \left(\frac{p}{1-p}\right)$$

Transformasi ini memiliki keuntungan bahwa rentang nilai log-odds berkisar dari negatif tak terbatas hingga positif tak terbatas, memberikan fleksibilitas yang baik dalam pemodelan.

Perlu diperhatikan bahwa istilah “logit” sendiri merujuk pada fungsi logaritmik dari odds \(\frac{p}{1-p}\)). Oleh karena itu, transformasi logit pada dasarnya adalah log-odds. Dengan demikian, meskipun keduanya terkait dan sering digunakan secara bersamaan, log-odds adalah konsep umum, sementara transformasi logit merujuk pada penerapan konsep tersebut dalam konteks spesifik Regresi Logistik.

c. Interpretasi Log-Odds dan Logit

#

Nilai log-odds menunjukkan seberapa besar perubahan dalam log-odds kejadian terjadi akibat perubahan dalam variabel independen. Ketika nilai log-odds dihasilkan, interpretasi dapat dilakukan untuk memahami sejauh mana variabel independen mempengaruhi probabilitas suatu kejadian.

Transformasi logit memainkan peran sentral dalam Regresi Logistik karena mengubah probabilitas menjadi skala log-odds yang dapat diinterpretasikan dengan lebih baik. Log-odds memberikan pemahaman tentang seberapa besar perubahan dalam probabilitas kejadian terjadi terkait dengan perubahan dalam variabel independen. Ini membantu kita untuk mengukur dan menginterpretasikan dampak variabel independen pada hasil kategorikal kita dengan cara yang konsisten.

Gambar berikut mengilustrasikan transformasi probabilitas menjadi skala log-odds menggunakan transformasi logit.

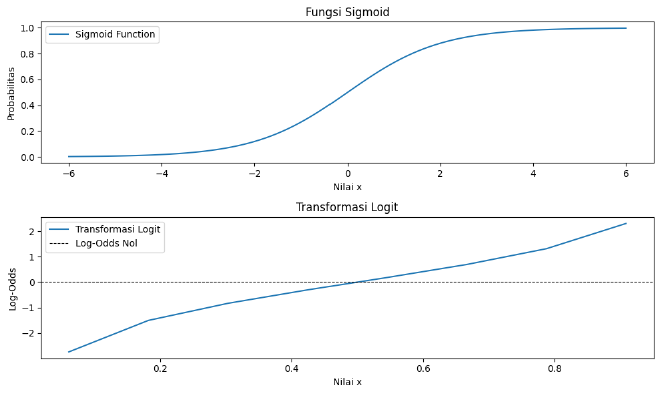
B. Fungsi Keputusan dan Probabilitas

#

Pada bagian ini kita akan mempelajari lebih dalam ke inti dari Regresi Logistik dengan memahami dua elemen utama, yaitu fungsi keputusan dan probabilitas. Fungsi keputusan, terutama diimplementasikan melalui fungsi sigmoid, memegang peran penting dalam pengambilan keputusan klasifikasi berdasarkan output model. Fungsi ini mengonversi nilai linier menjadi probabilitas, memungkinkan kita untuk menentukan kategori mana yang lebih mungkin. Sementara itu, interpretasi probabilitas menjadi kunci untuk memahami sejauh mana variabel independen memengaruhi hasil model. Pada bagian ini, kita akan membahas bagaimana fungsi keputusan dan probabilitas bekerja bersama untuk mengarahkan keputusan klasifikasi. Hal ini memberikan wawasan yang mendalam tentang proses pengambilan keputusan dalam Regresi Logistik.

1. Fungsi Sigmoid

#

Fungsi sigmoid adalah komponen sentral dalam Regresi Logistik. Fungsi ini digunakan untuk mengonversi nilai linier (\(z\)) menjadi probabilitas (\(p\)) dalam rentang 0 hingga 1. Fungsi sigmoid dinyatakan sebagai:

$$ \sigma(z) = \frac{1}{1 + e^{-z}} $$

dimana \(z\) merupakan nilai linier yang dihasilkan dari kombinasi linear variabel independen.

Fungsi Sigmoid bertujuan untuk menghasilkan nilai probabilitas yang dapat diinterpretasikan. Ketika \(z\) meningkat, probabilitas \(p\) mendekati 1; ketika \(z\) menurun, probabilitas \(p\) mendekati 0.

Penggunaan fungsi sigmoid dalam Regresi Logistik memiliki beberapa motivasi penting yang berkaitan dengan sifat dan kebutuhan model klasifikasi biner. Berikut adalah beberapa alasan utama:

1. Rentang Output Antara 0 dan 1

   Fungsi sigmoid menghasilkan output dalam rentang 0 hingga 1. Hal ini konsisten dengan interpretasi probabilitas, di mana nilai output mendekati 0 menunjukkan probabilitas rendah, sementara nilai mendekati 1 menunjukkan probabilitas tinggi. Dalam konteks Regresi Logistik, kita dapat menginterpretasikan output sebagai probabilitas kejadian suatu kategori.

2. Fungsi Monotonik dan Diferensial

   Sigmoid adalah fungsi monotonik yang berarti ketika nilai input meningkat, nilai output juga akan meningkat. Ini membuatnya cocok untuk digunakan dalam konteks optimisasi dan pembelajaran mesin. Selain itu, fungsi sigmoid adalah fungsi yang diferensial, memungkinkan penggunaan metode-metode optimasi berbasis gradien untuk menemukan parameter model yang optimal.

3. Representasi Log-Odds

   Fungsi sigmoid terkait dengan representasi log-odds melalui transformasi logit. Log-odds memberikan cara yang lebih baik untuk memodelkan hubungan antara variabel independen dan variabel dependen biner. Transformasi logit memungkinkan interpretasi yang lebih baik terhadap dampak variabel independen pada probabilitas.

4. Mudah Diinterpretasikan

   Output sigmoid dapat diinterpretasikan langsung sebagai probabilitas kejadian suatu kategori. Nilai yang mendekati 0.5 dapat diambil sebagai ambang batas (threshold) untuk pengambilan keputusan klasifikasi. Nilai output yang lebih besar dari 0.5 akan diklasifikasikan ke kategori 1, sementara nilai yang lebih kecil akan diklasifikasikan ke kategori 0.

5. Umum Digunakan

   Penggunaan sigmoid dalam Regresi Logistik telah menjadi standar di berbagai bidang, terutama dalam konteks klasifikasi biner. Keumuman ini membuatnya mudah diimplementasikan dan diinterpretasikan oleh praktisi dan peneliti di berbagai disiplin ilmu.

Secara keseluruhan, penggunaan sigmoid dalam Regresi Logistik didorong oleh kecocokannya dengan interpretasi probabilitas, sifat monotonik dan diferensialnya, serta kemudahan penggunaan dan interpretasi dalam konteks klasifikasi biner.

2. Interpretasi Probabilitas

#

Probabilitas (\(p\)) yang dihasilkan oleh fungsi sigmoid dalam Regresi Logistik memiliki peran sentral dalam pengambilan keputusan klasifikasi. Interpretasi probabilitas ini memungkinkan kita untuk memahami sejauh mana variabel independen mempengaruhi kemungkinan kejadian suatu kategori.

• Pemilihan Threshold (Ambang Batas)

  Ambang batas (0.5) umumnya digunakan untuk pengambilan keputusan klasifikasi. Jika \(p \gte 0.5\), maka observasi diklasifikasikan ke dalam kategori 1; sebaliknya, jika \(p \lt 0.5\), diklasifikasikan ke dalam kategori 0.

• Grafik Kurva Receiver Operating Characteristic (ROC)

  Kurva ROC membantu memahami trade-off antara sensitivity (true positive rate) dan specificity (true negative rate) dengan memvariasikan threshold. Ini membantu pemilihan threshold yang optimal berdasarkan kebutuhan spesifik aplikasi.

• Asumsi dan Pengaruh Threshold

  Memilih threshold tidak hanya bersifat teknis tetapi juga bergantung pada asumsi dan preferensi bisnis. Memilih threshold yang lebih rendah dapat meningkatkan sensitivity, sementara threshold yang lebih tinggi dapat meningkatkan specificity.

• Perluasan ke Multi-Kategori

  Dalam kasus multi-kategori, interpretasi probabilitas dapat diperluas dengan mempertimbangkan probabilitas untuk setiap kategori dan memilih kategori dengan probabilitas tertinggi.

Interpretasi probabilitas dalam Regresi Logistik memungkinkan kita untuk membuat keputusan klasifikasi yang relevan dan memahami dampak variabel independen pada hasil model. Pemilihan threshold adalah langkah kritis yang membutuhkan pertimbangan seksama sesuai dengan tujuan bisnis dan karakteristik masalah klasifikasi yang dihadapi. Menggunakan alat seperti kurva ROC dapat membantu melihat dampak dari variasi threshold terhadap performa model.