
Tahap-tahap Persiapan Data
Table of Contents
Persiapan Data untuk Machine Learning - This article is part of a series.
Pada tahap ini, kita akan membahas langkah-langkah esensial yang terlibat dalam persiapan data untuk machine learning menggunakan dataset “UCI ML Breast Cancer Wisconsin”. Setiap langkah memiliki peran penting dalam memastikan bahwa data yang digunakan untuk melatih dan menguji model machine learning kita berkualitas tinggi dan sesuai untuk tujuan analisis.
A. Pemahaman Data #
Sebelum kita memulai proses persiapan data, langkah pertama yang penting adalah memahami dataset dengan baik. Dengan memuat dataset “UCI ML Breast Cancer Wisconsin” kita akan mengeksplorasi beberapa baris pertama data, mengetahui informasi umum tentang dataset, dan melihat statistik deskriptif. Tujuan dari langkah ini adalah untuk mendapatkan wawasan awal tentang atribut-atribut yang ada. Pemahaman yang baik tentang data ini akan membentuk dasar untuk keputusan selanjutnya dalam persiapan data.
1. Profil Data Awal #
Profil data awal adalah langkah pertama dalam memahami dataset. Pada langkah ini, kita akan memuat dataset “UCI ML Breast Cancer Wisconsin” dan melakukan eksplorasi untuk mendapatkan wawasan tentang atribut-atribut yang ada. Tujuan dari langkah ini adalah untuk membentuk pemahaman awal tentang struktur dan karakteristik dataset, yang akan menjadi dasar bagi keputusan selanjutnya dalam persiapan data.
Contoh Kode:
from sklearn.datasets import load_breast_cancer
import pandas as pd
data = load_breast_cancer()
X, y = data.data, data.target
# Menampilkan beberapa baris pertama data
print(X[:5])
Berikut adalah hasil print:
[[1.799e+01 1.038e+01 1.228e+02 1.001e+03 1.184e-01 2.776e-01 3.001e-01
1.471e-01 2.419e-01 7.871e-02 1.095e+00 9.053e-01 8.589e+00 1.534e+02
6.399e-03 4.904e-02 5.373e-02 1.587e-02 3.003e-02 6.193e-03 2.538e+01
1.733e+01 1.846e+02 2.019e+03 1.622e-01 6.656e-01 7.119e-01 2.654e-01
4.601e-01 1.189e-01]
[2.057e+01 1.777e+01 1.329e+02 1.326e+03 8.474e-02 7.864e-02 8.690e-02
7.017e-02 1.812e-01 5.667e-02 5.435e-01 7.339e-01 3.398e+00 7.408e+01
5.225e-03 1.308e-02 1.860e-02 1.340e-02 1.389e-02 3.532e-03 2.499e+01
2.341e+01 1.588e+02 1.956e+03 1.238e-01 1.866e-01 2.416e-01 1.860e-01
2.750e-01 8.902e-02]
[1.969e+01 2.125e+01 1.300e+02 1.203e+03 1.096e-01 1.599e-01 1.974e-01
1.279e-01 2.069e-01 5.999e-02 7.456e-01 7.869e-01 4.585e+00 9.403e+01
6.150e-03 4.006e-02 3.832e-02 2.058e-02 2.250e-02 4.571e-03 2.357e+01
2.553e+01 1.525e+02 1.709e+03 1.444e-01 4.245e-01 4.504e-01 2.430e-01
3.613e-01 8.758e-02]
[1.142e+01 2.038e+01 7.758e+01 3.861e+02 1.425e-01 2.839e-01 2.414e-01
1.052e-01 2.597e-01 9.744e-02 4.956e-01 1.156e+00 3.445e+00 2.723e+01
9.110e-03 7.458e-02 5.661e-02 1.867e-02 5.963e-02 9.208e-03 1.491e+01
2.650e+01 9.887e+01 5.677e+02 2.098e-01 8.663e-01 6.869e-01 2.575e-01
6.638e-01 1.730e-01]
[2.029e+01 1.434e+01 1.351e+02 1.297e+03 1.003e-01 1.328e-01 1.980e-01
1.043e-01 1.809e-01 5.883e-02 7.572e-01 7.813e-01 5.438e+00 9.444e+01
1.149e-02 2.461e-02 5.688e-02 1.885e-02 1.756e-02 5.115e-03 2.254e+01
1.667e+01 1.522e+02 1.575e+03 1.374e-01 2.050e-01 4.000e-01 1.625e-01
2.364e-01 7.678e-02]]
Pada kode di atas, kita melakukan print 5 baris data pertama. Terlihat bahwa setiap baris memiliki 30 kolom. Kolom-kolom ini disebut juga dengan fitur. Mari kita lihat fitur apa saja yang ada dalam dataset ini:
# Informasi umum dataset
print(data.feature_names)
Berikut adalah hasilnya:
['mean radius' 'mean texture' 'mean perimeter' 'mean area'
'mean smoothness' 'mean compactness' 'mean concavity'
'mean concave points' 'mean symmetry' 'mean fractal dimension'
'radius error' 'texture error' 'perimeter error' 'area error'
'smoothness error' 'compactness error' 'concavity error'
'concave points error' 'symmetry error' 'fractal dimension error'
'worst radius' 'worst texture' 'worst perimeter' 'worst area'
'worst smoothness' 'worst compactness' 'worst concavity'
'worst concave points' 'worst symmetry' 'worst fractal dimension']
Hasil di atas menunjukan nama-nama fitur yang dimiliki oleh dataset ini. Kita dapat menggunakan fitur-fitur ini untuk melatih model machine learning.
Untuk melihat total data pada dataset ini, kita bisa menggunakan perintah len:
len(X)
Berikut adalah hasilnya
569
Hasil tersebut menunjukan bahwa total data pada dataset “UCI ML Breast Cancer Wisconsin” adalah 569 data.
2. Menentukan Variabel Target #
Variabel target, atau juga dikenal sebagai variabel respons atau label, adalah variabel akan diprediksi. Pada konteks machine learning, variabel target adalah nilai atau kategori yang ingin kita prediksi dengan memanfaatkan informasi dari variabel-variabel lain yang disebut sebagai variabel prediktor atau fitur.
Sebagai contoh, misalkan kita memiliki dataset mengenai pasien-pasien medis dengan berbagai atribut seperti usia, tekanan darah, dan tingkat kolesterol. Jika tujuan kita adalah untuk memprediksi apakah seorang pasien memiliki risiko penyakit jantung atau tidak, maka variabel yang menunjukkan apakah pasien tersebut memiliki penyakit jantung atau tidak akan menjadi variabel target.
Dalam permasalahan klasifikasi, variabel target sering kali bersifat kategorikal, seperti “positif” atau “negatif,” “ya” atau “tidak,” atau kategori lainnya. Sedangkan dalam permasalahan regresi, variabel target bersifat kontinu dan dapat berupa nilai-nilai dalam rentang tertentu.
Variabel target menjadi fokus utama dalam pengembangan model, karena kita ingin mengembangkan model yang dapat memberikan prediksi atau penjelasan yang akurat terhadap nilai atau kategori dari variabel ini.
Untuk dataset “UCI ML Breast Cancer Wisconsin”, variabel target sudah didefinisikan secara default. Kamu dapat mengakses variabel target menggunakan kode berikut:
print(data.target_names)
Berikut adalah hasilnya:
['malignant' 'benign']
Pada dataset “UCI ML Breast Cancer Wisconsin” terdapat dua kelas pada variabel target, yaitu ‘malignant’ (ganas) atau ‘benign’ (jinak). Kelas-kelas ini merepresentasikan kategori/jenis kanker payudara.
3. Analisis Statistik Deskriptif #
Analisis statistik deskriptif membantu kita mendapatkan gambaran yang lebih mendalam tentang distribusi variabel dalam dataset. Dengan melihat statistik deskriptif, kita dapat menemukan pola, kecenderungan, dan variabilitas data. Tujuan dari langkah ini adalah untuk mendapatkan wawasan statistik yang diperlukan untuk memahami sejauh mana variasi dan kecenderungan dalam data.
Kita dapat melihat statistik deskriptif dari sebuah dataset menggunakan bantuan library pandas. Pandas memiliki sebuah fungsi yang cukup powerful untuk menampilkan statistik deskriptif yaitu describe. Berikut adalah kodenya:
# Contoh kode
print(pd.DataFrame(X, columns=data.feature_names).describe())
Berikut adalah hasilnya:
mean radius mean texture mean perimeter mean area \
count 569.000000 569.000000 569.000000 569.000000
mean 14.127292 19.289649 91.969033 654.889104
std 3.524049 4.301036 24.298981 351.914129
min 6.981000 9.710000 43.790000 143.500000
25% 11.700000 16.170000 75.170000 420.300000
50% 13.370000 18.840000 86.240000 551.100000
75% 15.780000 21.800000 104.100000 782.700000
max 28.110000 39.280000 188.500000 2501.000000
mean smoothness mean compactness mean concavity mean concave points \
count 569.000000 569.000000 569.000000 569.000000
mean 0.096360 0.104341 0.088799 0.048919
std 0.014064 0.052813 0.079720 0.038803
min 0.052630 0.019380 0.000000 0.000000
25% 0.086370 0.064920 0.029560 0.020310
50% 0.095870 0.092630 0.061540 0.033500
75% 0.105300 0.130400 0.130700 0.074000
max 0.163400 0.345400 0.426800 0.201200
mean symmetry mean fractal dimension ... worst radius \
count 569.000000 569.000000 ... 569.000000
mean 0.181162 0.062798 ... 16.269190
std 0.027414 0.007060 ... 4.833242
min 0.106000 0.049960 ... 7.930000
25% 0.161900 0.057700 ... 13.010000
50% 0.179200 0.061540 ... 14.970000
75% 0.195700 0.066120 ... 18.790000
max 0.304000 0.097440 ... 36.040000
worst texture worst perimeter worst area worst smoothness \
count 569.000000 569.000000 569.000000 569.000000
mean 25.677223 107.261213 880.583128 0.132369
std 6.146258 33.602542 569.356993 0.022832
min 12.020000 50.410000 185.200000 0.071170
25% 21.080000 84.110000 515.300000 0.116600
50% 25.410000 97.660000 686.500000 0.131300
75% 29.720000 125.400000 1084.000000 0.146000
max 49.540000 251.200000 4254.000000 0.222600
worst compactness worst concavity worst concave points \
count 569.000000 569.000000 569.000000
mean 0.254265 0.272188 0.114606
std 0.157336 0.208624 0.065732
min 0.027290 0.000000 0.000000
25% 0.147200 0.114500 0.064930
50% 0.211900 0.226700 0.099930
75% 0.339100 0.382900 0.161400
max 1.058000 1.252000 0.291000
worst symmetry worst fractal dimension
count 569.000000 569.000000
mean 0.290076 0.083946
std 0.061867 0.018061
min 0.156500 0.055040
25% 0.250400 0.071460
50% 0.282200 0.080040
75% 0.317900 0.092080
max 0.663800 0.207500
[8 rows x 30 columns]
Pada contoh diatas, kita menggunakan fungsi describe untuk menampilkan statistik deskriptif untuk seluruh fitur. Terlihat bahwa fungsi describe mengembalikan matriks berukuran \(8 \times 30\), dimana \(30\) menunjukan jumlah fitur. Sedangkan \(8\) jumlah statistik deskriftif. Statistik ini meliputi: count (jumlah data), mean (rata-rata), std (standar deviasi), 25% (Q1), 50% (Q2), 75% (Q3) dan max (nilai maksimum). Melalui statistik deskriptif kita bisa melihat secara overall bagaimana sebaran tiap fitur pada dataset.
B. Data Cleaning (Pembersihan Data) #
Langkah penting berikutnya untuk memastikan kualitas dataset yang digunakan adalah pembersihan data. Pada tahap ini, kita akan mengidentifikasi dan menangani data yang mengandung nilai yang hilang, mendeteksi serta mengatasi outliers, dan membersihkan data dari kolom-kolom yang tidak relevan atau redundant. Motivasi di balik langkah ini adalah untuk memastikan dataset kita bebas dari anomali yang dapat mengganggu kinerja model, dan hanya menyisakan informasi yang relevan untuk analisis kita.
1. Identifikasi dan Penanganan Missing Value (Nilai yang Hilang) #
Identifikasi dan penanganan missing value termasuk langkah penting dalam persiapan data. Missing values dapat mengganggu analisis dan mempengaruhi kinerja model machine learning. Pada tahap ini, kita akan membahas bagaimana mengidentifikasi missing value dan strategi yang dapat digunakan untuk menangani situasi ini.
a. Identifikasi Missing Value #
Untuk mengidentifikasi missing value, kita bisa menggunakan fungsi isna() pada library pandas. Fungsi ini akan mengecek setiap sel pada dataframe apakah sel tersebut mengandung missing value atau tidak. Kemudian fungsi sum() digunakan mengagregasi jumlah sel yang mengandung missing value.
df = pd.DataFrame(X, columns=data.feature_names)
df.isna().sum()
Hasilnya adalah:
mean radius 0
mean texture 0
mean perimeter 0
mean area 0
mean smoothness 0
mean compactness 0
mean concavity 0
mean concave points 0
mean symmetry 0
mean fractal dimension 0
radius error 0
texture error 0
perimeter error 0
area error 0
smoothness error 0
compactness error 0
concavity error 0
concave points error 0
symmetry error 0
fractal dimension error 0
worst radius 0
worst texture 0
worst perimeter 0
worst area 0
worst smoothness 0
worst compactness 0
worst concavity 0
worst concave points 0
worst symmetry 0
worst fractal dimension 0
dtype: int64
Hasil di atas memperlihatkan bahwa tidak ada sel yang mengandung missing value.
b. Menangani Missing Value #
Jika terdapat data yang mengandung missing value, kamu bisa membuang data tersebut. Untuk membuat data yang mengandung missing value, kamu bisa menggunakan fungsi dropna pada pandas.
Contoh Kode:
# Contoh kode
clean_data = pd.DataFrame(X, columns=data.feature_names).dropna()
Pada kode di atas, kita membuang data yang mengandung missing value menggunakan fungsi dropna. Hasilnya adalah variabel baru clean_data yang tidak mengandung missing value.
Berikut adalah beberapa tujuan penanganan data yang mengandung missing value:
-
Mencegah Bias: Missing value dapat menyebabkan bias dalam analisis statistik atau prediksi model. Mengidentifikasi dan menangani missing value membantu meminimalkan bias ini.
-
Mengoptimalkan Kualitas Data: Data yang bersih dan lengkap dapat meningkatkan kualitas analisis dan prediksi. Penanganan missing value akan memastikan bahwa data yang digunakan untuk melatih model adalah data yang lengkap.
2. Mendeteksi dan Mengatasi Outlier #
Outlier adalah nilai-nilai ekstrem yang jauh berbeda dari mayoritas data. Keberadaan outlier dapat mempengaruhi analisis statistik dan dapat menjadi sumber distorsi jika tidak diatasi dengan tepat. Pada tahap ini, kita akan membahas cara mendeteksi outlier dan strategi yang dapat digunakan untuk mengatasi dampaknya pada model machine learning.
Mendeteksi dan mengatasi outlier membantu mencegah distorsi pada pembentukan model. Outlier dapat mempengaruhi performa model, dan langkah ini bertujuan untuk menjaga kestabilan dan keakuratan model dengan menangani nilai-nilai ekstrem.
Cara umum untuk menangai outlier adalah menggunakan skor Z untuk mengukur seberapa jauh suatu nilai dari rata-rata dalam satuan standar deviasi.
a. Mengenal Z-Score (Skor Z) #
Z-score atau skor z adalah ukuran statistik yang dapat digunakan untuk menilai seberapa jauh nilai individu dalam suatu distribusi dari rata-rata (mean) distribusi dalam satuan standar deviasi. Skor Z dihitung dengan rumus:
\[ Z = \frac{{x - \mu}}{{\sigma}} \]
di mana:
- \(x\) adalah nilai individu,
- \(\mu\) adalah rata-rata distribusi, dan
- \(\sigma\) adalah standar deviasi distribusi.
Dalam konteks deteksi outlier, skor Z digunakan karena memiliki sifat yang menggambarkan seberapa besar nilai suatu observasi berada jauh dari rata-rata distribusi dalam satuan standar deviasi. Beberapa alasan mengapa skor Z efektif dalam mendeteksi outlier adalah:
-
Standardisasi Data: Skor Z mengubah distribusi data menjadi distribusi standar normal dengan mean 0 dan standar deviasi 1. Ini memungkinkan perbandingan yang lebih mudah antara nilai-nilai dari distribusi yang berbeda.
-
Batasan Kriteria: Penelitian statistik umumnya menggunakan aturan empiris seperti “68-95-99.7 rule” atau “empat aturan sembilan” untuk menentukan seberapa dekat nilai-nilai tertentu dengan mean dalam distribusi normal standar. Nilai-nilai yang sangat jauh dari mean (misalnya, skor Z yang melebihi 3 atau -3) dapat dianggap sebagai outlier.
-
Memungkinkan Penyesuaian Threshold: Dengan menggunakan nilai ambang tertentu untuk skor Z, kita dapat menyesuaikan kepekaan deteksi outlier. Nilai ambang yang lebih tinggi akan lebih ketat dan lebih memilih hanya outlier yang sangat ekstrem.
b. Cara Mendeteksi Outlier #
Salah satu cara untuk mendeteksi outlier adalah menggunakan visualisasi boxplot. Visualisasi boxplot memberikan gambaran visual seputar distribusi data dan membantu kita mengidentifikasi nilai-nilai yang jauh dari kuartil. Outlier dapat terlihat sebagai titik-titik yang berada di luar “whiskers” (jangkauan interkuartil).
Boxplot adalah salah satu metode visualisasi data yang berguna untuk menunjukkan distribusi, letak pusat, serta adanya outlier dalam dataset. Hubungan antara skor Z dan boxplot terkait dengan deteksi outlier.
Pada boxplot, ada konsep yang disebut sebagai batas atas (upper fence) dan batas bawah (lower fence) yang membantu mengidentifikasi outlier. Batas atas dan batas bawah ditentukan dengan menggunakan IQR (Interquartile Range), yang merupakan perbedaan antara kuartil atas (Q3) dan kuartil bawah (Q1). Outlier diidentifikasi sebagai nilai yang berada di luar batas atas dan batas bawah, yang dihitung sebagai berikut:
\[ \text{Upper Fence} = Q3 + 1.5 \times \text{IQR} \] \[ \text{Lower Fence} = Q1 - 1.5 \times \text{IQR} \]
Jika nilai dalam dataset melewati batas atas atau batas bawah, maka nilai tersebut dianggap sebagai outlier.
Pada kode berikut, kita akan melakukan deteksi outlier pada fitur “mean radius”.
# Visualisasi boxplot
import seaborn as sns
sns.boxplot(x=clean_data['mean radius'])
Berikut adalah hasilnya:
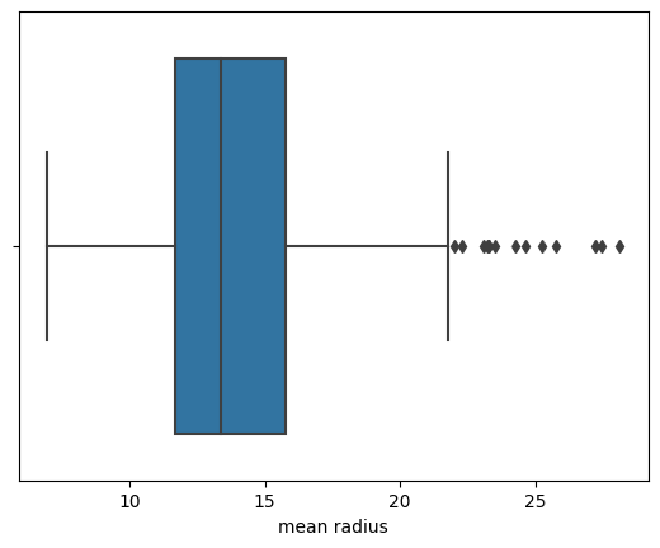
Interpretasi grafik di atas adalah sebagai berikut:
- Pada boxplot, garis tengah kotak mewakili median.
- Kotak biru (interkuartil) mencakup kuartil pertama (Q1) hingga kuartil ketiga (Q3).
- Whiskers menunjukkan rentang nilai yang dapat dianggap normal.
- Titik-titik di luar whiskers dapat dianggap sebagai outlier.
Pada grafik di atas, terlihat bahwa terdapat beberapa titik outlier pada fitur “mean radius”. Kamu bisa mencoba sendiri untuk mendeteksi outlier pada feature yang lainnya.
c. Menangani Data Outlier #
Setelah mengetahui adanya outlier dalam data, langkah selanjutnya adalah menangani data outlier tersebut. Terdapat beberapa strategi untuk menangani data outlier:
-
Jika data outlier jumlahnya terbatas dan tidak signifikan, kita dapat menghapus nilai-nilai outlier tersebut. Berikut adalah contoh kode untuk menghapus outlier.
# Contoh kode from scipy import stats z_scores = stats.zscore(clean_data) data_no_outliers = clean_data[(z_scores < 3).all(axis=1)] -
Melakukan transformasi data, seperti log-transform, untuk mengurangi dampak outlier.
Transformasi data merujuk pada penggunaan operasi matematis atau fungsi matematika tertentu untuk mengubah nilai-nilai data dalam usaha untuk mengurangi dampak atau efek dari outlier. Transformasi data dapat membantu membuat distribusi data lebih simetris, menyesuaikan variabilitas, dan membuat data lebih cocok untuk analisis statistik atau pemodelan. Berikut ini adalah contoh kode untuk mentransformasi fitur “mean radius” menggunakan log-transform.
# Log-transform untuk mengurangi dampak outliers import numpy as np data['mean radius'] = np.log1p(data['mean radius']) -
Mengganti nilai-nilai outlier dengan nilai batas atas atau batas bawah yang ditentukan (Winsorizing).
Selain dua cara di atas, kita juga bisa mengganti nilai-nilai outlier dengan batas atas atau batas bawah. Fungsi
winsorizedari library scipy dapat digunakan untuk keperluan tersebut.# Winsorizing pada batas bawah dan atas from scipy.stats.mstats import winsorize data['mean radius'] = winsorize(data['mean radius'], limits=[0.05, 0.05])
3. Membersihkan Data yang Redundan atau Tidak Relevan #
Data yang redundan atau tidak relevan merujuk pada fitur atau kolom dalam dataset yang tidak memberikan nilai tambah signifikan terhadap tujuan analisis atau prediksi model. Secara umum, atribut dapat dianggap redundan atau tidak relevan jika:
-
Korelasi Tinggi: Fitur memiliki korelasi tinggi satu sama lain, sehingga memberikan informasi yang serupa. Dalam kasus ini, salah satu dari fitur tersebut dapat dianggap tidak relevan karena memberikan informasi yang hampir identik dengan fitur lain.
-
Variansi Rendah: Fitur memiliki variasi yang sangat rendah, artinya nilainya tidak berubah banyak antara satu sampel data dengan sampel yang lain. Fitur dengan variasi rendah mungkin tidak memberikan kontribusi signifikan dalam proses analisis atau prediksi.
-
Informasi Serupa: Dua atau lebih fitur memberikan informasi yang esensialnya sama atau saling tumpang tindih sehingga tidak ada peningkatan signifikan dalam pemahaman data ketika fitur tersebut digunakan bersamaan.
-
Tidak Berkaitan dengan Tujuan Analisis: Fitur tidak memiliki hubungan yang signifikan dengan tujuan analisis atau prediksi model. Meskipun fitur tersebut mungkin memiliki variasi atau informasi, jika tidak relevan dengan tujuan tertentu, dapat dianggap tidak berguna.
Membersihkan data dari fitur atau kolom yang redundan atau tidak relevan adalah langkah penting dalam persiapan data. Fitur yang tidak memberikan kontribusi signifikan terhadap tujuan analisis atau prediksi model sebaiknya dihapus untuk menyederhanakan dataset. Pada tahap ini, kita akan membahas cara mengidentifikasi dan mengatasi data yang redundan atau tidak relevan.
Berikut adalah cara mengidentifikasi data yang redundan atau tidak relevan:
-
Analisis Korelasi:
Menggunakan matriks korelasi untuk mengevaluasi hubungan antar fitur. Fitur yang memiliki korelasi tinggi dapat dianggap redundan. Untuk melihat korelasi antar fitur, kamu dapat menggunakan fungsi
corrpada pandas. Perhatikan contoh kode berikut:# Menghitung matriks korelasi correlation_matrix = clean_data.corr()Fungsi ini akan mengembalikan matrik korelasi. Matriks ini berisi korelasi antara seluruh fitur yang ada. Kita dapat dengan mudah melihat mana fitur-fitur yang memiliki korelasi tinggi satu sama lain.
-
Analisis Varian:
Untuk mengidentifikasi relevansi sebuah fitur, kita dapat menggunakan analisis varian. Analisis varian berfungsi untuk menilai variasi antar fitur. Fitur dengan variasi rendah tidak akan memberikan informasi yang signifikan sehingga bisa dihapus. Untuk melihat variasi tiap fitur, kamu bisa menggunakan fungsi
varpada pandas. Perhatikan contoh kode berikut:# Menghitung varians atribut variances = clean_data.var()
Berikut adalah cara mengatasi data yang redundan atau tidak relevan:
-
Penghapusan Fitur:
Setelah mengetahui bahwa sebuah fitur redundan atau tidak relevan, kita dapat menghapus fitur tersebut. Untuk menghapus fitur, kamu dapat menggunakan fungsi
droppada pandas. Perhatikan contoh berikut.# Menghapus atribut dengan korelasi tinggi data_no_redundant = clean_data.drop(['mean data'], axis=1)Pada contoh kode di atas, kita melakukan penghapusan pada fitur “mean data”.
-
Menggabung Fitur:
Selain itu, kamu juga bisa menggabung fitur yang memiliki informasi serupa untuk membuat fitur baru yang lebih relevan. Perhatikan contoh kode berikut:
# Menggabungkan beberapa fitur menjadi satu clean_data['mean radius texture'] = clean_data['mean radius'] + clean_data['mean texture']Pada contoh di atas, kita menambahkan fitur “mean radius” dan “mean texture” menjadi satu fitur gabungan yaitu “mean radius texture”.

